안녕하세요 Coding-Knowjam입니다.
오늘은 그래프 알고리즘인 위상 정렬을 Java로 구현해보겠습니다.
1. 위상 정렬(Topological Sort)이란?
1.1 개념
우리가 알고리즘을 공부할 때 그래프에 관련된 문제를 많이 접하게 됩니다.
위상 정렬(Topological Sort) 또한 그래프와 관련된 알고리즘 중 하나입니다.
그렇다면 위상 정렬(Topological Sort)은 언제 사용할까요??
바로 선후관계가 정의된 그래프 구조에서 정렬을 하기 위해 사용할 수 있습니다.
글로만 보면 이해가 잘 되지 않으실 테니 그림과 함께 설명하겠습니다.

위와 같은 그래프가 있을 때, 노드마다 연결된 간선에 방향이 있고 어떤 특정 노드를 방문하기 위해서는 해당 노드에 진입 가능한 노드들을 모두 방문한 후에 방문이 가능하다고 가정해보겠습니다.
그렇다면 현재 그래프의 선후관계는 다음과 같습니다.
| 1번 노드 | 2번 노드 | 3번 노드 | 4번 노드 | 5번 노드 | 6번 노드 | 7번 노드 | 8번 노드 |
| 없음 | 1번 노드 4번 노드 |
7번 노드 | 1번 노드 | 2번 노드 | 2번 노드 3번 노드 8번 노드 |
없음 | 4번 노드 |
이러한 선후관계가 존재할 때, 노드를 방문하는 순서를 찾아야 한다면 위상 정렬을 사용할 수 있습니다.
또한 예를 들어 그래프가 어떠한 물건의 생산 흐름이라고 하면 각각의 노드들이 특정한 작업이 되고, 이때 작업의 순서를 구해야 한다면 위상 정렬을 사용할 수 있습니다.
추가적으로 위상 정렬의 결과 값은 여러 가지가 존재할 수 있습니다.
왜냐하면 어떠한 작업에 대해 선후관계가 정해져 있지 않다면 어느 것을 먼저 해도 상관이 없기 때문입니다.
한 가지 유의해야 할 점은 위상 정렬(Topological Sort)을 사용하기 위해서는 그래프가 순환하지 않아야 합니다.
예를 들어 아래 그림과 같이 1번, 2번, 4번 노드끼리 순환구조가 생긴다면 위상 정렬을 사용할 수 없습니다.

즉, 비순환 그래프 DAG(Directed Acyclic Graph)이어야 사용할 수 있습니다.
그럼 위상 정렬(Topological Sort)은 어떤 순서로 진행되는지 알아보겠습니다.
1.2 위상 정렬 진행순서
위상 정렬을 수행하는 방법은 큐 또는 재귀 함수를 사용하는 것입니다.
일반적으로 큐를 사용해서 많이 구현하므로 저도 큐를 사용할 때를 기준으로 설명드리겠습니다.
진행순서는 다음과 같습니다.
- 그래프의 각 노드들의 진입 차수 테이블 생성 및 진입 차수 계산
- 진입 차수가 0인 노드 큐에 넣기 (이때 어떤 노드 먼저 시작하던지 관계없음)
- 큐에서 노드를 하나 꺼낸 후 꺼낸 노드와 간선으로 연결된 노드들의 진입 차수 감소 (진입 차수 테이블 갱신)
- 진입 차수 테이블을 갱신 후 진입 차수의 값이 0인 노드가 있다면 큐에 넣기 (없으면 아무것도 안 함)
- 3~4번의 순서를 큐에 더 이상 아무것도 없을 때까지 반복
위와 같은 순서로 위상 정렬(Topological Sort)은 수행되며, 모든 순서가 끝났는데도 진입 차수가 0이 아닌 노드가 있다면 그래프 내에서 순환이 존재한다고 볼 수 있습니다.
글로만 보면 이해가 잘 안 되시니 앞에서 예시로 들었던 그래프와 같이 진행순서를 살펴보겠습니다.
1. 그래프의 각 노드들의 진입 차수 테이블 생성 및 진입 차수 계산
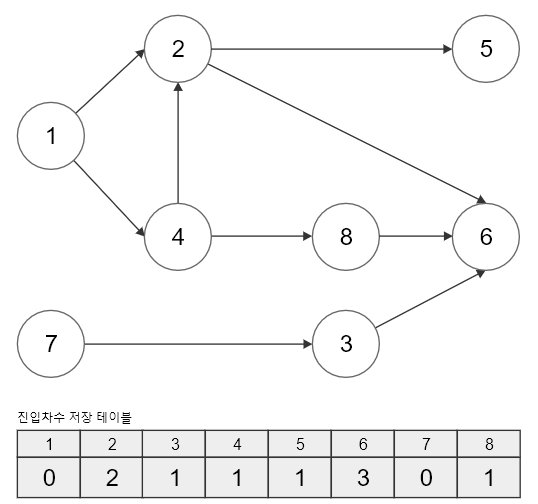
위의 그림은 앞에서 봤던 예시 그래프의 선후관계를 고려해서 진입 차수 테이블을 생성한 상태입니다.
앞에서 선후관계를 나타냈던 테이블을 기억하시나요?
그 테이블에서의 노드 개수가 결국 진입 차수와 같은 의미입니다.
2번과 6번 노드를 예로 들어서 보겠습니다.
2번 노드의 경우 1번과 4번 노드를 방문해야만 갈 수 있으므로 진입 차수가 2가 됩니다.
6번 노드의 경우 2번, 8번, 3번 노드를 방문해야만 갈 수 있으므로 진입 차수가 3이 됩니다.
이러한 형태로 초기에는 진입 차수 테이블을 초기화해주시면 됩니다.
2. 진입 차수가 0인 노드 큐에 넣기 (이때 어떤 노드 먼저 시작하던지 관계없음)
이제 진입 차수가 0인 노드들을 찾아서 큐에 넣어주면 됩니다.
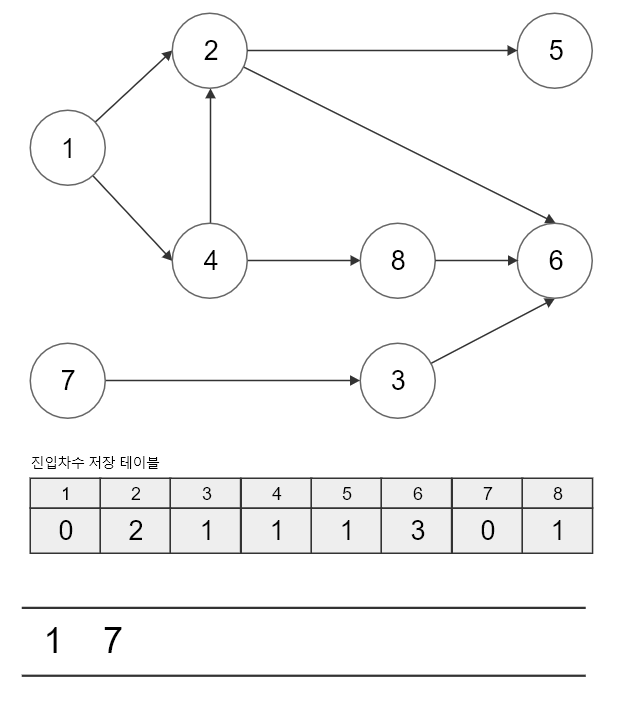
진입 차수가 0인 노드는 1번과 7번이므로 큐에 넣으면 위의 그림과 같이 표현할 수 있습니다.
3. 큐에서 노드를 하나 꺼낸 후 꺼낸 노드와 간선으로 연결된 노드들의 진입 차수 감소 (진입 차수 테이블 갱신)
4. 진입 차수 테이블을 갱신 후 진입 차수의 값이 0인 노드가 있다면 큐에 넣기 (없으면 아무것도 안 함)
이제 큐에서 노드를 하나 꺼낸 후 진입 차수 테이블을 갱신시켜보겠습니다.
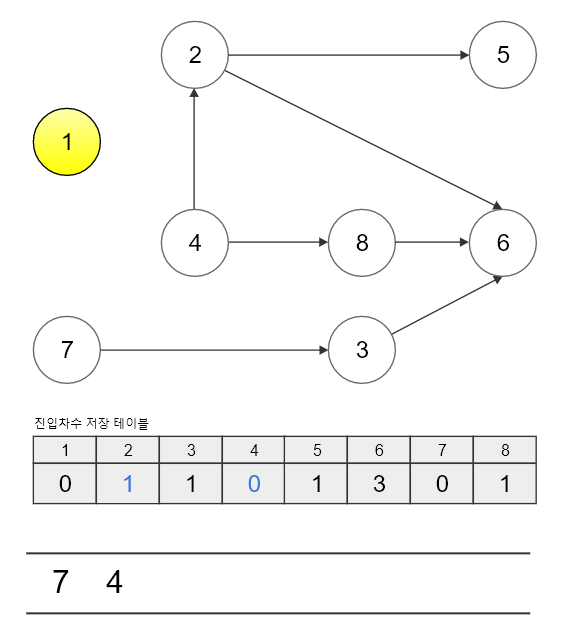
우선 큐에서 1번 노드를 꺼내고 인접한 노드들을 찾습니다.
앞서 1번 노드에서는 2번과 4번 노드로 간선이 연결되어 있었습니다.
그러므로 2번과 4번 노드의 진입 차수를 1씩 감소시켜줍니다. (이는 1번 노드의 간선이 제거되는 것과 같은 의미이므로 그림에서는 간선을 제거했습니다.)
이 과정이 진입 차수 테이블을 갱신하는 과정입니다.
갱신이 끝났으면 2번과 4번 노드의 진입 차수가 0인지 확인을 합니다.
만약에 0이라면 큐에 넣어주고 아니라면 다음 순서로 넘어갑니다.
이번 갱신에서는 4번 노드의 진입 차수가 0이 되었으므로 큐에 넣어줍니다.
현재까지 정렬의 결과는 아래와 같습니다.
현재까지 결과 : 1 ->?
5. 3~4번의 순서를 큐에 더 이상 아무것도 없을 때까지 반복
말 그대로 반복하면 되므로 정렬을 계속 진행해보겠습니다.

이제 큐에서 7번 노드를 꺼내고 인접한 노드들을 찾습니다.
7번 노드는 3번 노드와 간선으로 연결되어있으므로 3번 노드의 진입 차수를 1씩 감소시켜줍니다. (이는 3번 노드의 간선이 제거되는 것과 같은 의미이므로 그림에서는 간선을 제거했습니다.)
갱신이 끝났으면 3번 노드의 진입 차수가 0인지 확인을 합니다.
만약에 0이라면 큐에 넣어주고 아니라면 다음 순서로 넘어갑니다.
이번 갱신에서는 3번 노드의 진입 차수가 0이 되었으므로 큐에 넣어줍니다.
현재까지 정렬의 결과는 아래와 같습니다.
현재까지 결과 : 1 -> 7 ->?
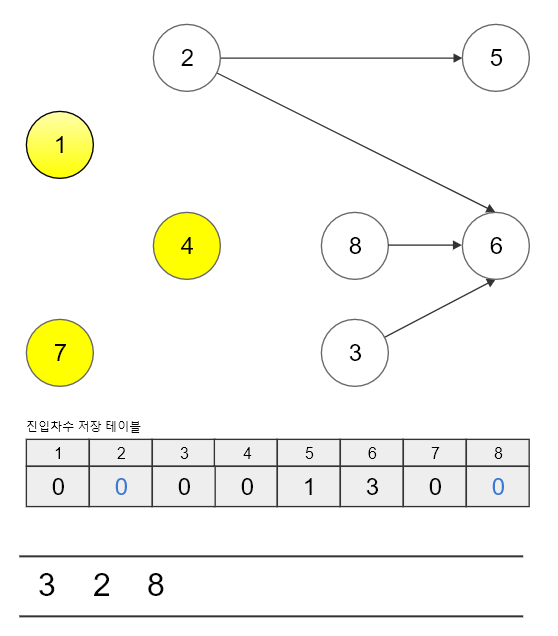
큐에서 4번 노드를 꺼내고 인접한 노드들을 찾아 진입 차수 테이블을 갱신시켜줍니다.
갱신이 끝났으면 2번, 8번 노드의 진입 차수가 0인지 확인을 합니다.
만약에 0이라면 큐에 넣어주고 아니라면 다음 순서로 넘어갑니다.
이번 갱신에서는 2개의 인접한 노드 모두 진입 차수가 0이 되었으므로 큐에 전부 넣어줍니다.
큐에 넣는 순서는 2,8로 넣든 8,2로 넣든 상관이 없습니다.
저는 오름차순으로 넣어 주겠습니다.
현재까지 결과 : 1 -> 7 -> 4 ->?

큐에서 3번 노드를 꺼내고 인접한 노드들을 찾아 진입 차수 테이블을 갱신시켜줍니다.
갱신된 노드의 진입 차수가 0이라면 큐에 넣어주고 아니라면 다음 순서로 넘어갑니다.
현재까지 결과 : 1 -> 7 -> 4 -> 3 ->?

큐에서 2번 노드를 꺼내고 인접한 노드들을 찾아 진입 차수 테이블을 갱신시켜줍니다.
갱신된 노드의 진입 차수가 0이라면 큐에 넣어주고 아니라면 다음 순서로 넘어갑니다.
현재까지 결과 : 1 -> 7 -> 4 -> 3 -> 2 ->?
큐에서 8번 노드를 꺼내고 인접한 노드들을 찾아 진입 차수 테이블을 갱신시켜줍니다.
갱신된 노드의 진입 차수가 0이라면 큐에 넣어주고 아니라면 다음 순서로 넘어갑니다.
현재까지 결과 : 1 -> 7 -> 4 -> 3 -> 2 -> 8 ->?

큐에서 5번 노드를 꺼내고 인접한 노드들을 찾아 진입 차수 테이블을 갱신시켜줍니다.
5번 노드의 경우 현재 인접한 노드가 존재하지 않으므로 테이블의 갱신은 일어나지 않습니다.
갱신이 일어나지 않았다면 큐에 넣을 노드는 존재하지 않으므로 이 과정은 생략됩니다.
현재까지 결과 : 1 -> 7 -> 4 -> 3 -> 2 -> 8 -> 5 ->?
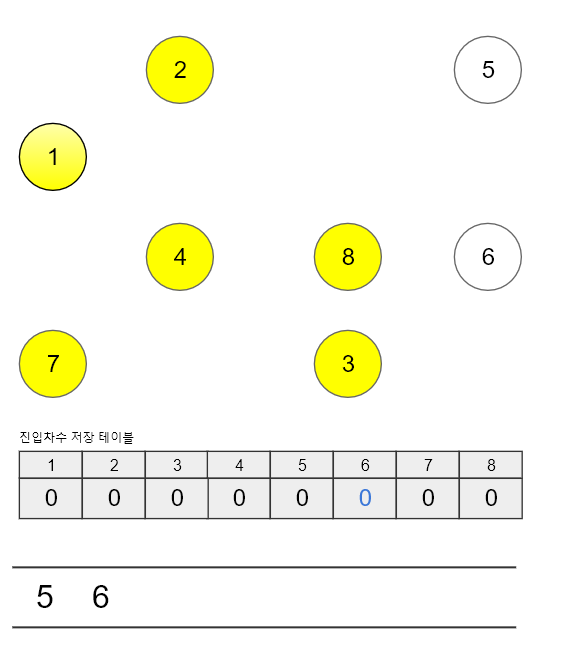
마지막으로 큐에서 6번 노드를 꺼내고 인접한 노드들을 찾아 진입 차수 테이블을 갱신시켜줍니다.
6번 노드의 경우 현재 인접한 노드가 존재하지 않으므로 테이블의 갱신은 일어나지 않습니다.
갱신이 일어나지 않았다면 큐에 넣을 노드는 존재하지 않으므로 이 과정은 생략됩니다.
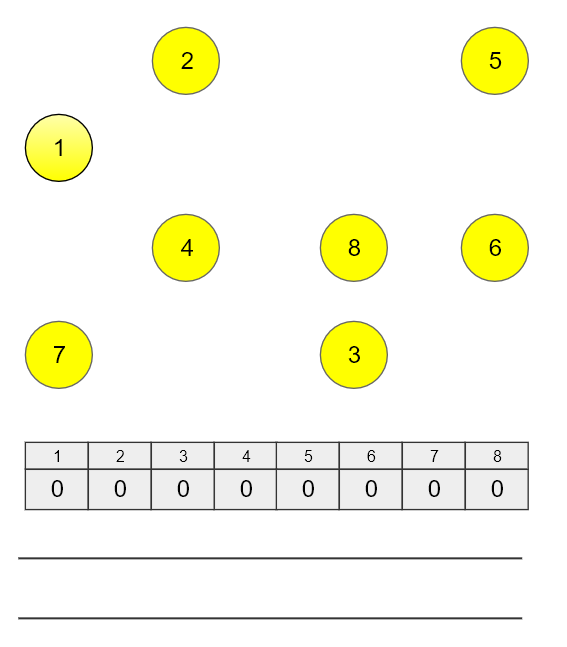
현재까지 결과 : 1 -> 7 -> 4 -> 3 -> 2 -> 8 -> 5 -> 6
이제 모든 과정이 끝나고 큐가 비었습니다.
큐가 비었을 때 모든 노드들의 진입 차수 또한 0 이여야 합니다.
진입 차수가 0이 아닌 노드가 존재한다면 그래프에 순환구조가 있다는 얘기이므로 위상 정렬을 사용할 수 없습니다.
위상 정렬을 수행한 결과는 다음과 같습니다.
위상 정렬 수행 결과 : 1 -> 7 -> 4 -> 3 -> 2 -> 8 -> 5 -> 6
앞서 말씀드렸지만 위상 정렬의 결과는 여러 가지가 존재할 수 있습니다.
예를 들어 5번과 6번 노드의 순서가 바뀌어도 상관이 없습니다.
왜냐하면 5번과 6번은 서로 선후관계가 아니기 때문입니다.
그러므로 1 -> 7 -> 4 -> 3 -> 2 -> 8 -> 6 -> 5의 결과가 존재할 수도 있습니다.
이제 위상 정렬(Topological Sort)을 코드로 작성해보겠습니다.
2. 위상 정렬(Topological Sort)을 Java코드로 구현
package study.blog.codingnojam.algorithm;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class Study_topologicalSort {
public static void main(String[] args) throws IOException {
// 위상정렬 결과를 출력할 객체
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 위상정렬에 사용할 진입차수 저장 배열
// 길이가 9인 이유는 인덱스를 1부터 사용하기 위해서입니다.
int[] edgeCount =new int[9];
// 위상정렬에 사용할 그래프 2차원 리스트로 구현
ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i < 9; i++) {
graph.add(new ArrayList<Integer>());
}
// 그래프 각 노드별 인접한 노드정보 초기화
graph.get(1).add(2);
graph.get(1).add(4);
graph.get(2).add(5);
graph.get(2).add(6);
graph.get(3).add(6);
graph.get(4).add(2);
graph.get(4).add(8);
graph.get(7).add(3);
graph.get(8).add(6);
// 진입차수 테이블 초기화
edgeCount[2] = 2;
edgeCount[3] = 1;
edgeCount[4] = 1;
edgeCount[5] = 1;
edgeCount[6] = 3;
edgeCount[8] = 1;
// 위상정렬에 사용할 큐
Queue<Integer> q = new LinkedList<>();
// 진입차수가 0인 값 큐에 넣기
for (int i = 1; i < edgeCount.length; i++) {
if (edgeCount[i] == 0) {
q.offer(i);
}
}
// 큐가 빌 때까지 반복
while (!q.isEmpty()) {
// 큐에서 노드번호 꺼내기
int nodeNo = q.poll();
// 꺼낸 노드번호 정렬 결과값에 저장
bw.write(String.valueOf(nodeNo) + " ");
// 꺼낸 노드의 인접한 노드들 찾기
List<Integer> list = graph.get(nodeNo);
// 인접한 노드의 개수만큼 반복문 실행
for (int i = 0; i < list.size(); i++) {
// 인접한 노드 진입차수 갱신
edgeCount[list.get(i)] -- ;
// 갱신된 노드의 진입차수가 0이면 큐에 노드 넣기
if (edgeCount[list.get(i)] == 0) {
q.offer(list.get(i));
}
}
}
// 위상정렬 수행 결과 값 출력
bw.flush();
}
}
작성한 코드의 모든 라인마다 주석을 적었습니다.
앞에서 그림과 같이 설명했던 대로 구현을 했기 때문에 코드와 주석을 같이 보시면 이해하는데 어렵지 않으실 겁니다.
예제 코드에서는 그래프를 초기화할 때 값을 직접 리스트에 add 해주었지만 실제 코딩 테스트에서는 주어진 입력값을 받아서 초기화를 하셔야 합니다.
감사합니다.
'Algorithm & Data Structure > 이론' 카테고리의 다른 글
| [Algorithm] 유클리드 호제법을 Java로 구현해보자!! (with BOJ 2609) (1) | 2021.07.21 |
|---|---|
| [Algorithm] 세그먼트 트리(Segment Tree)를 Java로 구현해보자! !(with BOJ-2042 Java로 문제풀이) (0) | 2021.06.13 |
| [Algorithm] 다익스트라(Dijkstra) 알고리즘을 Java로 구현해보자! (BOJ-1753 최단경로) (0) | 2021.04.20 |
| [Algorithm] DFS (Depth-first Search)를 Java로 구현해보자! (7) | 2021.04.16 |
| [Algorithm] BFS(Breadth-first search)를 Java로 구현해보자! (3) | 2021.04.11 |


댓글